Reti neurali feedforward

L'architettura più semplice

Ecco una nuova puntata della serie di articoli dedicati alla matematica delle reti neurali.

Nello scorso articolo ho introdotto il concetto di rete neurale, e ne abbiamo visto gli elementi principali. Se te lo fossi perso, lo puoi leggere qui:

In questo articolo andremo ad approfondire la più semplice tipologia di rete neurale, ovvero le reti neurali feedforward.

Prima di avventurarci nei dettagli, ricordiamo che una rete neurale è semplicemente una funzione parametrica che solitamente è definita tramite la composizione di funzioni più elementari. Possiamo pensare queste funzioni elementari come dei blocchetti lego che impiliamo uno sopra l’altro, per ottenere l’architettura della rete neurale. Questi elementi costitutivi vengono chiamati strati o layer della rete neurale.

Definizione dei layer della rete

In base a come i layer/strati vengono definiti, otteniamo diverse tipologie di reti neurali. La più semplice è quella feedforward, dove i layer sono della seguente forma

\(F_{\theta_\ell}(x) = \sigma(A_\ell x + b_\ell),\,\,\ell=1,...,L,\,\sigma:\mathbb{R}\to\mathbb{R}.\)

Nell’articolo precedente sono stato appositamente un po’ vago sulle dimensioni dei pesi, mentre ora voglio dare qualche dettaglio in più.

Supponiamo che l’input abbia d entrate, e che vogliamo approssimare una funzione

\(f:\mathbb{R}^d\to\mathbb{R}^c\)

per qualche c. La nostra rete dovrà essere definita in modo che

\(\mathcal{N}_\theta:\mathbb{R}^d\to\mathbb{R}^c.\)

Di conseguenza, se

\(\mathcal{N}_\theta = F_{\theta_L}\,\circ\, ...\, \circ\, F_{\theta_1},\)

possiamo vincolare le dimensioni dei layer intermedi come segue:

\(A_\ell \in\mathbb{R}^{c_{\ell}\times c_{\ell-1}},\,b_\ell\in\mathbb{R}^{c_{\ell}},\,\ell=1,...,L,\,\,c_0 = d,\,c_{L}=c.\)

Funzione di attivazione

La funzione di attivazione

\(\sigma,\)

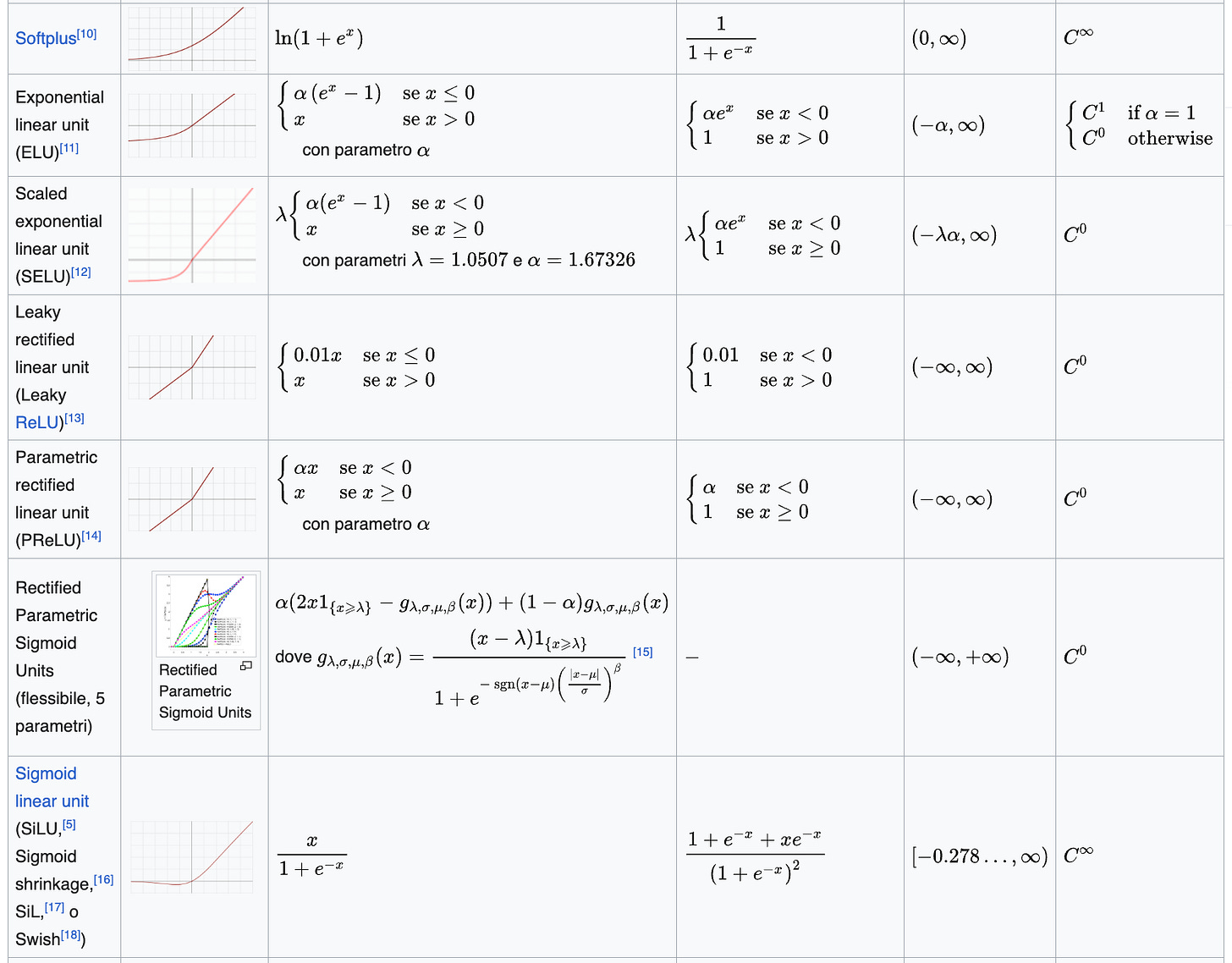
a volte chiamata non-linearità, può essere una qualunque funzione scalare. Tuttavia, ci sono alcune scelte più comuni di altre. Le principali sono raccolte nella seguente tabella (che ho copiato dalla pagina Wikipedia)

Tipicamente ogni layer della rete usa la stessa funzione di attivazione. Tuttavia niente ci vieta di sperimentare con architetture un po’ più “stravaganti”. Vedremo anche in futuro che sostanzialmente per ogni funzione di attivazione è possibile mostrare che ogni funzione continua può essere approssimata arbitrariamente bene da reti come sopra.

Ho già dedicato un articolo alla funzione ReLU, che è una delle più popolari, e lo trovi qui:

Reti profonde (deep) e reti shallow

La rete si dice profonda se ha più di un layer con una non-linearità. Una rete non profonda (o deep) si dice shallow. Le reti shallow si esprimono in modo più semplice come

\(\mathcal{N}_\theta(x) = A_2 \sigma(A_1x+b_1)+b_2.\)

L’alternanza tra funzioni parametriche affini e non-linearità applicate componente per componente caratterizza praticamente ogni rete neurale. È però abbastanza comune comporre l’ultimo layer con un’ulteriore funzione affine che ci permette di non finire con una non linearità. Dato che questa scelta dipende in modo sostanziale dall’applicazione in analisi, non ci soffermiamo su questo aspetto per il momento. Questa casistica può anche essere vista come una rete dove l’ultima funzione di attivazione è la funzione identità. Per questo motivo, non serve preoccuparsi particolarmente di questa variante.

Matrici dei pesi dense o sparse

Le matrici dei pesi

\(A_1,...,A_L\)

possono essere matrici piene oppure possono essere sparse, dipendentemente dall’applicazione di interesse. Per esempio, quando si lavora con delle immagini, è comune sostituire le funzioni affini dense con degli operatori di convoluzione, per i quali le matrici diventano di Toeplitz o circolanti. Se questi termini ti sono nuovi, non preoccuparti perché dedicherò un intero articolo a questa tipologia di reti.

Prima di chiudere con questa breve descrizione delle reti feedforward, voglio lasciarti con un semplice esempio e ad una breve sezione con del codice PyTorch dove implemento l’architettura vista sopra. L’esempio l’ho scelto in modo da “ripassare” anche alcune delle proprietà della funzione ReLU che ho menzionato nell’articolo dedicato.

Codice

Qui sotto puoi trovare una semplice implementazione con PyTorch dell’architettura di cui abbiamo parlato fino ad ora. Non mi soffermo più di tanto a commentare il codice, dato che puoi trovare già molte risorse online che ne descrivono i dettagli, oppure aiutarti con qualche servizio tipo ChatGPT per capire meglio cosa viene fatto.

import torch
import torch.nn as nn

class RetiFeedForward(nn.Module):
    """
    𝒩_θ = F_{θ_L} ∘ … ∘ F_{θ_1}
    con F_{θ_ℓ}(x) = σ(A_ℓ x + b_ℓ).

    d : dim. input,  c : dim. output,  L : #layer,
    h = d + 2        (dim. nascosta fissa)
    """
    def __init__(self, d: int, c: int, L: int,
                 act: str = "relu", last_act: bool = False):
        super().__init__()
        if L < 1:
            raise ValueError("L deve essere ≥ 1")

        h = d + 2                       # hidden dimension richiesta

        # Mappa ‹nome› → modulo; .lower() rende la chiave indifferente  al maiuscolo/minuscolo.
        # .get(…, nn.ReLU()) restituisce ReLU se la chiave non esiste.
        attivazioni = {
            "relu": nn.ReLU(),
            "tanh": nn.Tanh(),
            "sigmoid": nn.Sigmoid(),
            "gelu": nn.GELU()
        }
        self.σ = attivazioni.get(act.lower(), nn.ReLU())

        layers = []
        if L == 1:
            layers.append(nn.Linear(d, c))
        else:
            layers.append(nn.Linear(d, h))      # primo
            for _ in range(L - 2):              # intermedi
                layers.append(nn.Linear(h, h))
            layers.append(nn.Linear(h, c))      # ultimo

        self.moduli   = nn.ModuleList(layers)
        self.L        = L
        self.last_act = last_act

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        for i, lin in enumerate(self.moduli):
            x = lin(x)                          # A_ℓ x + b_ℓ
            if i < self.L - 1 or self.last_act: # applica σ dove serve
                x = self.σ(x)
        return x

Esempio

Consideriamo la funzione

\(f:\mathbb{R}^3\to\mathbb{R},\,\,f(x_1,x_2,x_3)=\max\{x_1,x_2\}+x_3.\)

Iniziamo ricordando che

\(\max\{x_1,x_2\} = x_1 + \mathrm{ReLU}(x_2-x_1),\)

e anche che

\(x_1 = \mathrm{ReLU}(x_1)-\mathrm{ReLU}(-x_1).\)

Queste considerazioni ci permettono di scrivere

\(\begin{split} \max\{x_1,x_2\} &= \mathrm{ReLU}(x_1)-\mathrm{ReLU}(-x_1) + \mathrm{ReLU}(x_2-x_1) \\& = \begin{bmatrix} 1 & -1 & 1\end{bmatrix}\,\mathrm{ReLU}\left(\begin{bmatrix} 1 &0 &0 \\ -1 & 0 & 0 \\ -1 & 1 & 0\end{bmatrix}x\right),\,\,x = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}\in\mathbb{R}^3. \end{split}\)

Notiamo quindi che il massimo tra due numeri può essere espresso come una rete neurale shallow basata sulla ReLU come funzione di attivazione.

Con un ragionamento analogo, possiamo anche esprimere f come segue

\(f(x_1,x_2,x_3) = A_2 \mathrm{ReLU}(A_1x),\,\,x = \begin{bmatrix} x_1\\ x_2 \\ x_3\end{bmatrix}\in\mathbb{R}^3,\)

dove

\(A_1 = \begin{bmatrix} 1 & 0 & 0 \\ -1 & 0 & 0\\ -1 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & -1 \end{bmatrix}\in\mathbb{R}^{5\times 3},\,\,A_2 = \begin{bmatrix} 1 & -1 & 1 & 1 & - 1 \end{bmatrix} \in\mathbb{R}^5.\)

Esercizio

Per esercizio ti consiglio di provare ad esprimere come rete neurale feedforward la seguente funzione

\(f(x_1,x_2,x_3) = \min\{x_1,|x_2-x_3|\}.\)

Suggerimento: Pensa a come scrivere il valore assoluto tramite la funzione ReLU.