Metodo di discesa del gradiente

Nel post di oggi andiamo avanti con la serie di articoli sulle reti neurali, e rimaniamo concentrati sull’ottimizzazione della funzione di costo. Nel post precedente, che trovi qui sotto, abbiamo visto il metodo di discesa del gradiente nel caso scalare.

Oggi, con l’aiuto del video che ho pubblicato ormai 5 anni fa su YouTube, e che trovi associato a questo post, vediamo di generalizzarlo a funzioni vettoriali.

Prima di proseguire con l’algoritmo e la descrizione qui sotto, ti consiglio fortemente di guardare il video perchè credo che l’intuizione grafica e geometrica sia molto più facile da comprendere lì che nelle formule qui sotto.

Descrizione dell’algoritmo

Consideriamo una funzione

\(f:\mathbb{R}^n\to\mathbb{R}\)

regolare abbastanza. Ti ricordo che il gradiente di una funzione scalare in un punto x è un vettore che ha tante entrate quante le componenti di x, dove le entrate corrispondo alle derivate parziali rispetto alle corrispondenti componenti:

\(\nabla f(x) = \begin{bmatrix} \partial_{x_1}f(x) & \dots & \partial_{x_n}f(x)\end{bmatrix}^\top, \,x=\begin{bmatrix} x_1 & \dots & x_n \end{bmatrix}^\top .\)

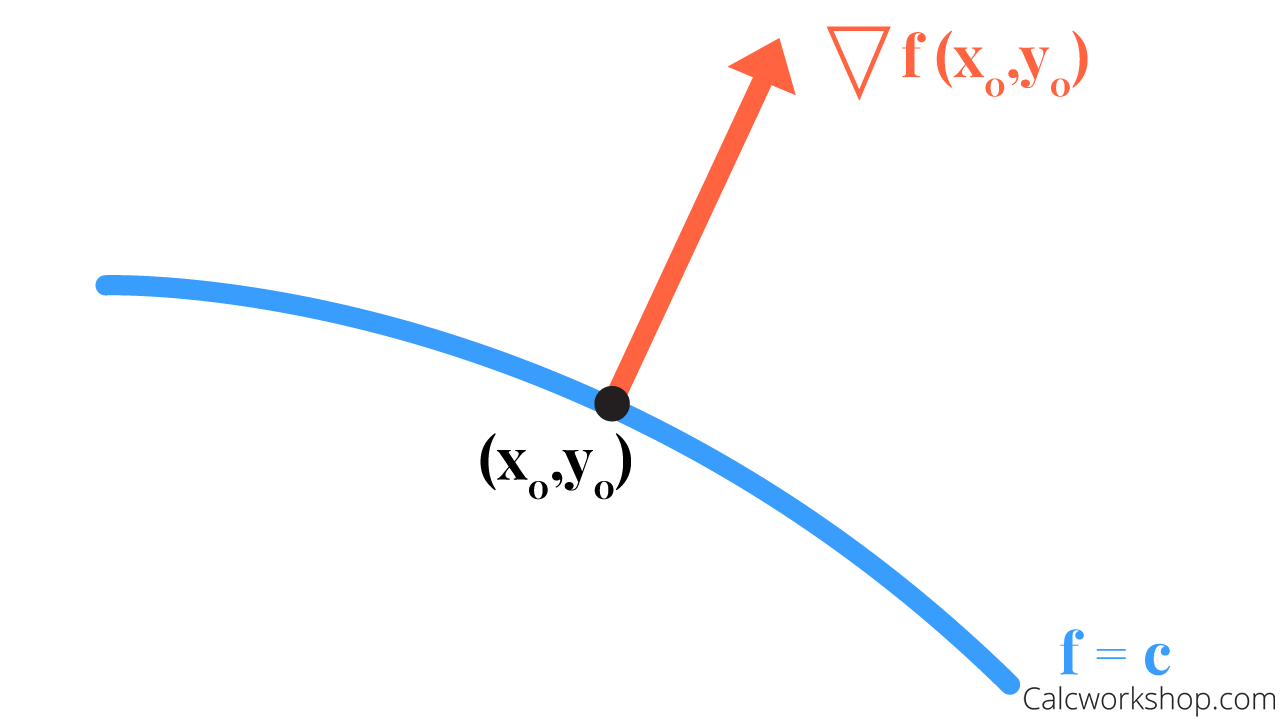
Probabilmente già sai che il gradiente di una funzione scalare in un punto determina la direzione ortogonale all’insieme livello di quel punto.

Ti ricordo inoltre che l’insieme di livello di un punto x è definito come segue

\(L_x = \{y\in\mathbb{R}^n:\,\,f(x)=f(y)\}\subseteq\mathbb{R}^n.\)

Notiamo inoltre che, usando l’espansione in serie di Taylor intorno ad un punto x, si può scrivere

\(f(x+v) = f(x) + v^\top \nabla f(x) + \mathcal{O}(\|v\|_2^2),\,v\in\mathbb{R}^n,\)

dove

\(\mathcal{O}(\|v\|_2^2)\)

è una notazione per raccogliere tutti i termini che dipendono almeno quadraticamente da v. Supponendo che v sia abbastanza piccolo, possiamo quindi trascurare questi termini quadratici, e approssimare la funzione in un punto x+v con il valore che essa ha in x a cui dobbiamo aggiungere un termine che dipende sia da v che dal gradiente nel punto x.

La cosa interessante, a questo punto, è notare che nel caso in cui v sia allineato con il gradiente di f in x, andremo a massimizzare la variazione della funzione, dato che per la disuguaglianza di Cauchy-Schwarz vale che

\(v^\top \nabla f(x) = \cos(v,\nabla f(x))\|v\|_2\|\nabla f(x)\|_2\)

dove il coseno è dell’angolo compreso tra i due vettori. Per cui, dato che il coseno vale 1 per l’angolo zero, notiamo che se v punta nella direzione del gradiente di f in x, avremo il coseno massimo. Similmente, nel caso la direzione sia questa ma il verso sia opposto, otteniamo un angolo tra i due vettori di 180°, e quindi un coseno di -1.

Ricordiamo ora che il nostro interesse è risolvere il seguente problema di minimizzazione:

\(\min_{x\in\mathbb{R}^n}f(x).\)

Il ragionamento fatto sopra, ci suggerisce quindi che andare nella direzione opposta del gradiente di f in un punto potrebbe essere una buona idea. Infatti questa scelta, almeno localmente, ci permette di ottenere la massima decrescita del valore della funzione. Siamo quindi pronti per introdurre il metodo della discesa del gradiente.

L’algoritmo

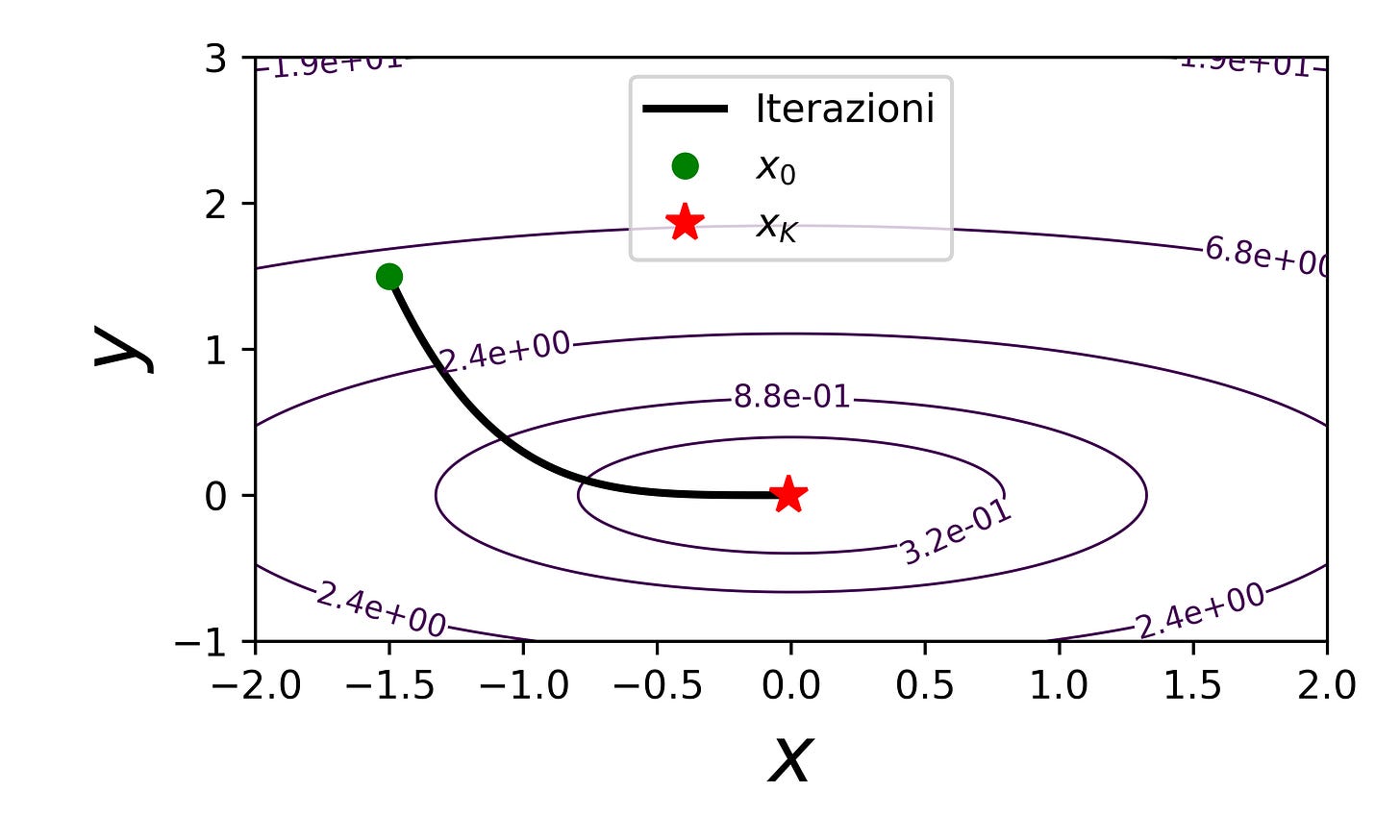
Come nel caso scalare, il metodo di discesa del gradiente è un metodo iterativo. Ciò vuol dire che partiamo da una posizione iniziale ragionevole o casuale x_0, e cerchiamo pian piano di migliorarla. Il processo continua fino a quando non raggiungiamo un livello desiderabile di approssimazione del minimo.

L’algoritmo è quindi definito come segue:

\(\begin{split} x_0&\in\mathbb{R}^n\\ x_{k+1} &= x_k - \tau \nabla f(x_k),\,\,\tau \in [0,2/L),\,k=0,1,2,... \end{split}\)

dove L>0 è la costante di Lipschitz del gradiente, ovvero

\(\|\nabla f(y) - \nabla f(x)\|_2 \leq L\|y-x\|_2,\,\,\forall x,y\in\mathbb{R}^n.\)

In questo articolo non andremo a vedere perchè sia necessario questo limite superiore del passo tau. Dedicheremo uno dei prossimi articoli a questo tema.

Ci tengo però a far notare che il metodo non fa altro che cercare di diminuire il valore attuale della funzione, f(x_k), andando nella direzione che, localmente, ci fornisce la massima decrescita. Il passo tau ci permette di controllare quanto ci allontaniamo dalla posizione attuale, e, intuitivamente, non possiamo prenderlo troppo grande perchè altrimenti smettiamo di avere a che fare con una direzione di decrescita.

Dietro il vincolo che 0<tau<2/L c’è l’ipotesi che il gradiente di f sia L-Lipschitz. Questa è spesso accoppiata all’ipotesi che f sia (strettamente) convessa, per garantire l’esistenza (e unicità) di un minimo globale e tassi di convergenza ottimali del metodo. Per ora non mi ci soffermo molto, ma dedicherò il prossimo articolo ad introdurre cosa sia una funzione convessa, e poi andremo a vedere le proprietà di convergenza del metodo nel successivo.

Esempio semplice

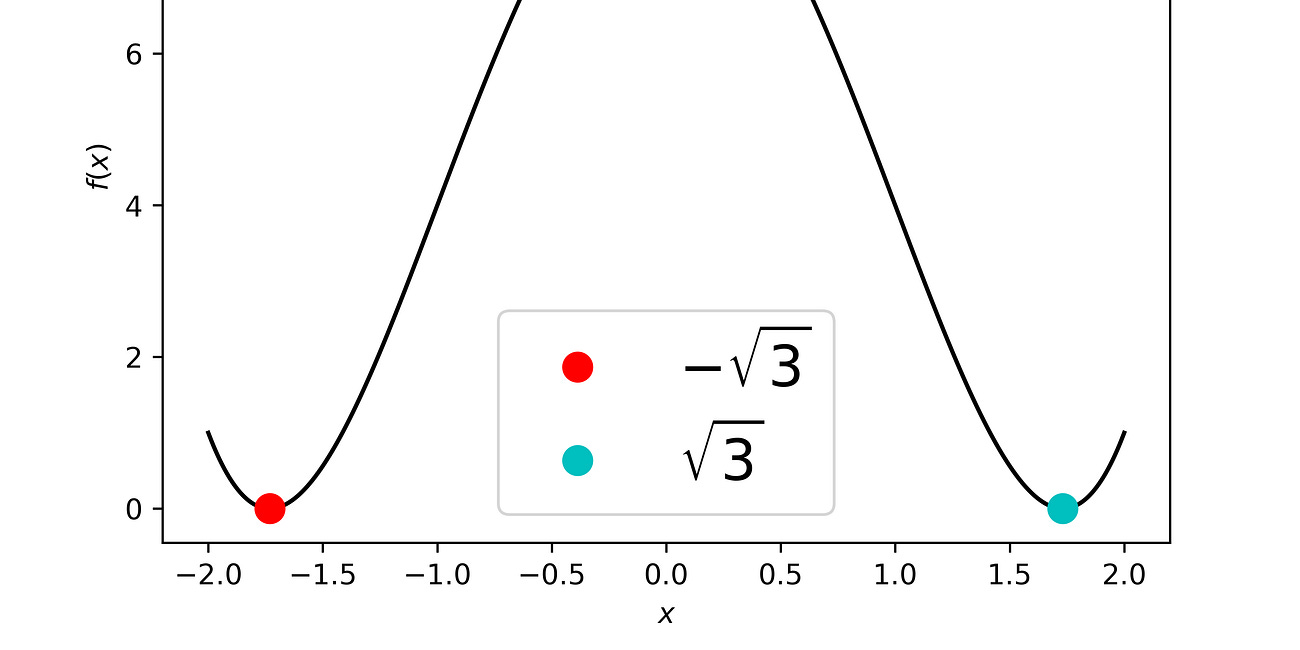
Consideriamo un esempio semplice, ovvero

\(f(x)=\|x\|_2^2/2,\,x\in\mathbb{R}^n,\,\,\|x\|_2^2 = x^\top x = x_1^2+...+x_n^2.\)

Il gradiente di f è il seguente

\(\nabla f(x) = x\in\mathbb{R}^n,\)

che è una funzione 1-Lipschitz, ovvero L=1, dato che

\(\|\nabla f(y)-\nabla f(x)\|_2=\|y-x\|_2\leq \|y-x\|_2.\)

Ciò significa che il metodo di discesa del gradiente in questo caso diventa

\(\begin{split} x_0&\in\mathbb{R}^n\\ x_{k+1} &= x_k - \tau \nabla f(x_k) = x_k - \tau x_k = (1-\tau)x_k,\,\,\tau \in [0,2). \end{split}\)

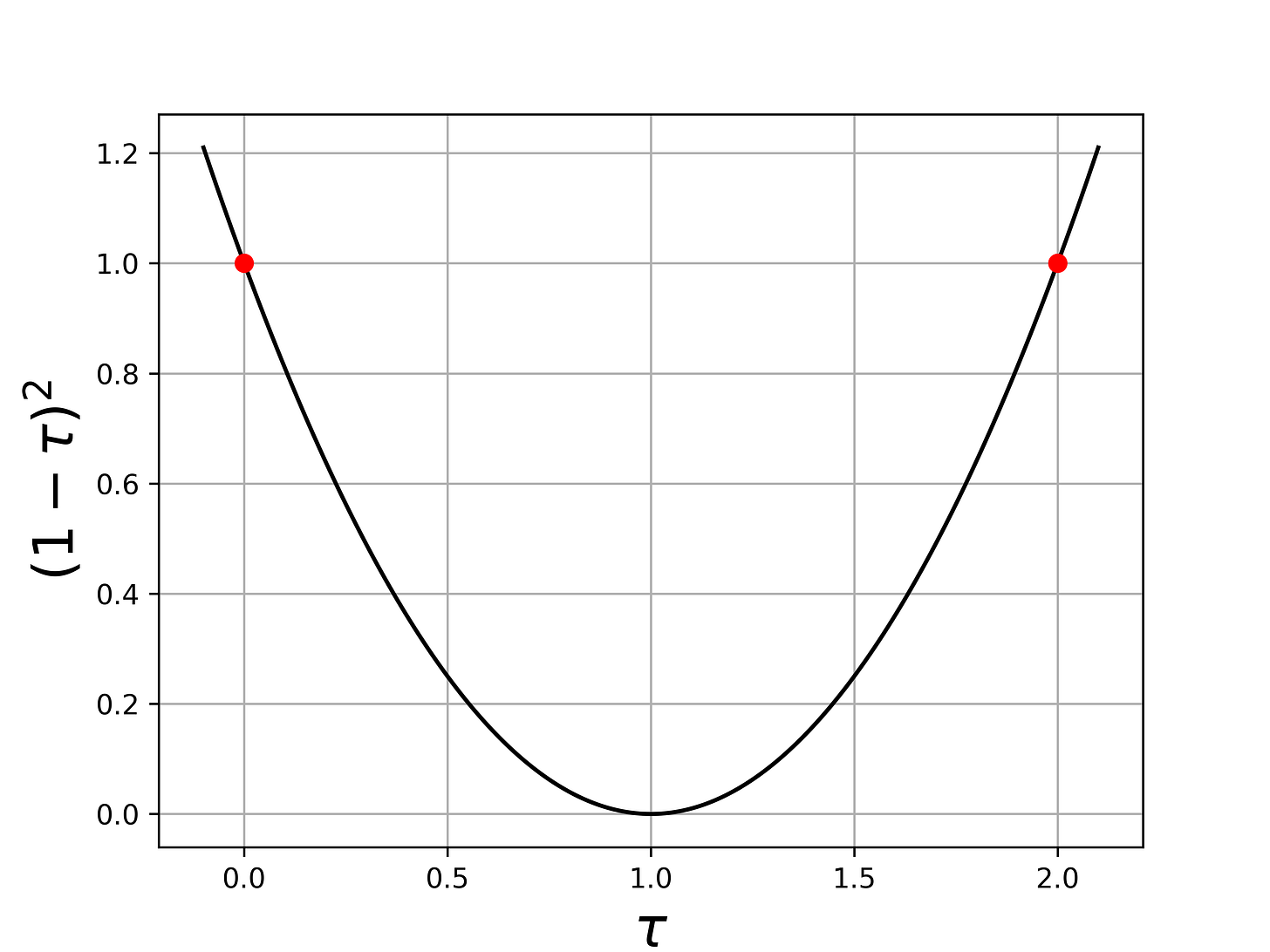
Qui iniziamo ad intuire il perchè del vincoli che tau sia minore di 2, dato che se non lo fosse non andremmo a diminuire la norma. Infatti, abbiamo che

\(f(x_{k+1})=\frac{1}{2}\|x_{k+1}\|_2^2 = \frac{(1-\tau)^2}{2}\|x_k\|_2^2 = (1-\tau)^2 f(x_k),\)

e la funzione (1-tau)^2 è più piccola di 1 solo se tau è tra 0 e 2:

Prendiamo per esempio tau=0.5, quindi il metodo diventa

\(x_{k} = \frac{1}{2}x_{k-1} = \left(\frac{1}{2}\right)^kx_0,\)

e quindi si vede che se consideriamo il criterio d’arresto

\(\|\nabla f(x_k)\|_2 \leq \varepsilon,\)

andremo a fare

\(\begin{split} &\left(\frac{1}{2}\right)^K \|x_0\|_2 \leq \varepsilon \\ &\iff -K\log(2)\leq \log\left(\frac{\varepsilon}{\|x_0\|_2}\right) \\ &\iff K\geq \frac{1}{\log{2}}\log\left(\frac{\|x_0\|_2}{\varepsilon}\right) \end{split}\)

passi.

Conclusione

Spero che l’articolo ti sia risultato piacevole ed interessante! Se hai domande scrivi pure nei commenti che cerco di leggere frequentemente.